~/dev/on

Programming, music, machine learning, etc.

Numerical Computing With Scala

In the previous post, we looked at the Fourier transform function. In this post, we’ll explore some implementations of this function in Scala and capture some performance metrics.

Before we start, we need a data representation for complex numbers and a pure trait to test different FFT functions. Note that the FFT trait specifies a Numeric type class so it can work with any sequence of numbers.

1
2
3
4
5

case class Complex(r: Double, i: Double = 0.0) {
  def +(x: Complex) = Complex(r + x.r, i + x.i)
  def -(x: Complex) = Complex(r - x.r, i - x.i)
  def *(x: Complex) = Complex(r * x.r - i * x.i, r * x.i + i * x.r)
}

1
2
3

trait FFT {
  def fft[A : Numeric](data: Seq[A]): Seq[Complex]
}

As mentioned in the previous post, the Cooley-Turkey algorithm requires that the data length be a power of 2. All of our equations in the previous post were in terms of the complex exponential function (eix). Using Euler’s formula we can instead rely on sine and cosine functions in our implementations.

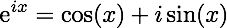
Recursive Implementation

The recursive nature of the standard Cooley-Turkey algorithm lends itself nicely to a pure functional implementation. Since we should always prefer pure functional code, we’ll start there.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

object CooleyTurkey extends FFT {
  import scala.math._

  def fft[A](data: Seq[A])(implicit num: Numeric[A]): Seq[Complex] = {
    require((data.length & data.length - 1) == 0)

    ditfft2(data map { a => Complex(num.toDouble(a)) })
  }

  private[this] def ditfft2(data: Seq[Complex]): Seq[Complex] = {
    data.length match {
      case 0 => Nil
      case 1 => data
      case n => {
        val evens = ditfft2(filterByIndex(data) { _ % 2 == 0 })
        val odds = ditfft2(filterByIndex(data) { _ % 2 != 0 })
        val phase = for (i <- 0 to n / 2 - 1) yield {
          val p = -2.0 * Pi * i / n
          Complex(cos(p), sin(p))
        }

        val ops = (odds, phase).zipped map { _ * _ }
        val one = (evens, ops).zipped map { _ + _ }
        val two = (evens, ops).zipped map { _ - _ }

        one ++ two
      }
    }
  }

  private[this] def filterByIndex[A](a: Seq[A])(p: Int => Boolean) =
    a.zipWithIndex filter { t => p(t._2) } map { t => t._1 }
}

This actually follows the mathematical definition pretty nicely and is very concise and readable. Note that we are recursively breaking the data into smaller DFTs by even and odd indexes. We’re calculating the phase (twiddle) factors seperately and relying on the symmetric properties of the DFT to recombine the values for 0 ≤ k < N/2 and N/2 ≤ k < N.

So how well does this algorithm perform? First try with 1024 random Double values on my machine takes ~ 100 ms. OK, let’s see how this does once the machine warms up. If we try 10 random sequences in a row (size 1024), we get:

We can see that it’s starting to settle. After running 1000 iterations, we get an average of ~ 3 ms per fft call.

Imperative Implementation

It’s no secret that optimizing Scala code can sometimes be ugly (see Erik Osheim’s Premature Optimization). So let’s see if we move towards an imperative version of the FFT.

The following is basically a translation of the algorithm from Apache Commons-Math into Scala. This algorithm is still based on the Cooley-Turkey algorithm, but the implementation is much more verbose and harder to follow than the recursive version.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122

object ApacheFFT extends FFT {
  import scala.math._

  def fft[A](data: Seq[A])(implicit num: Numeric[A]): Seq[Complex] = {
    require((data.length & data.length - 1) == 0)

    val real = (data map { num.toDouble(_) }).toArray
    val imag = Array.ofDim[Double](data.length)
    inPlaceFFT(real, imag)
    (real, imag).zipped map { Complex(_, _) }
  }

  private[this] lazy val W_SUB_N_R = (0 to 64) map { i => cos(2 * Pi / pow(2, i)) }
  private[this] lazy val W_SUB_N_I = (0 to 64) map { i => -sin(2 * Pi / pow(2, i)) }

  private[this] def bitReverseShuff(real: Array[Double], imag: Array[Double]) {
    val n = real.length
    val halfOfN = n >> 1

    def swap(dv: Array[Double], a: Int, b: Int) = {
      val tmp = dv(a)
      dv(a) = dv(b)
      dv(b) = tmp
    }

    var i, j = 0
    while (i < n) {
      if (i < j) {
        swap(real, i, j)
        swap(imag, i, j)
      }

      var k = halfOfN
      while (k <= j && k > 0) {
        j -= k
        k >>= 1
      }
      j += k
      i += 1
    }
  }

  private[this] def inPlaceFFT(real: Array[Double], imag: Array[Double]) {
    val n = real.length

    bitReverseShuff(real, imag)

    var i0 = 0
    while (i0 < n) {
      val i1 = i0 + 1
      val i2 = i0 + 2
      val i3 = i0 + 3

      val srcR0 = real(i0)
      val srcI0 = imag(i0)
      val srcR1 = real(i2)
      val srcI1 = imag(i2)
      val srcR2 = real(i1)
      val srcI2 = imag(i1)
      val srcR3 = real(i3)
      val srcI3 = imag(i3)

      real(i0) = srcR0 + srcR1 + srcR2 + srcR3
      imag(i0) = srcI0 + srcI1 + srcI2 + srcI3

      real(i1) = srcR0 - srcR2 + (srcI1 - srcI3)
      imag(i1) = srcI0 - srcI2 + (srcR3 - srcR1)

      real(i2) = srcR0 - srcR1 + srcR2 - srcR3
      imag(i2) = srcI0 - srcI1 + srcI2 - srcI3

      real(i3) = srcR0 - srcR2 + (srcI3 - srcI1)
      imag(i3) = srcI0 - srcI2 + (srcR1 - srcR3)

      i0 += 4
    }

    var lastN0 = 4
    var lastLogN0 = 2
    var n0, logN0 = 0
    var wSubN0R, wSubN0I, wSubN0ToRR, wSubN0ToRI, grR, grI, hrR, hrI, nextWsubN0ToRR, nextWsubN0ToRI = 0.0
    while (lastN0 < n) {
      n0 = lastN0 << 1
      logN0 = lastLogN0 + 1
      wSubN0R = W_SUB_N_R(logN0)
      wSubN0I = W_SUB_N_I(logN0)

      var destEvenStartIndex = 0
      while (destEvenStartIndex < n) {
        val destOddStartIndex = destEvenStartIndex + lastN0
        wSubN0ToRR = 1.0
        wSubN0ToRI = 0.0

        var r = 0
        while (r < lastN0) {
          grR = real(destEvenStartIndex + r)
          grI = imag(destEvenStartIndex + r)
          hrR = real(destOddStartIndex + r)
          hrI = imag(destOddStartIndex + r)

          real(destEvenStartIndex + r) = grR + wSubN0ToRR * hrR - wSubN0ToRI * hrI
          imag(destEvenStartIndex + r) = grI + wSubN0ToRR * hrI + wSubN0ToRI * hrR

          real(destOddStartIndex + r) = grR - (wSubN0ToRR * hrR - wSubN0ToRI * hrI)
          imag(destOddStartIndex + r) = grI - (wSubN0ToRR * hrI + wSubN0ToRI * hrR)

          nextWsubN0ToRR = wSubN0ToRR * wSubN0R - wSubN0ToRI * wSubN0I
          nextWsubN0ToRI = wSubN0ToRR * wSubN0I + wSubN0ToRI * wSubN0R
          wSubN0ToRR = nextWsubN0ToRR
          wSubN0ToRI = nextWsubN0ToRI

          r += 1
        }

        destEvenStartIndex += n0
      }

      lastN0 = n0
      lastLogN0 = logN0
    }
  }
}

Yikes, we went from 30 lines of code to 120. Let’s take a look at a few points in this algorithm though. Since we are no longer recursively selecting even/odd indexes, we perform a bit-reverse shuffle of the data up front. This allows us to traverse the data in essentially the same order. Also, note that the WNk real and imaginary factors are pre-computed. This, in combination with the fact that we are operating on arrays and avoiding boxing and unboxing will certainly make this algorithm faster. Let’s see how much.

Using the same test as before, our first try with 1024 random samples takes ~ 20 ms. Next up, let’s test with the warmup using 10 iterations:

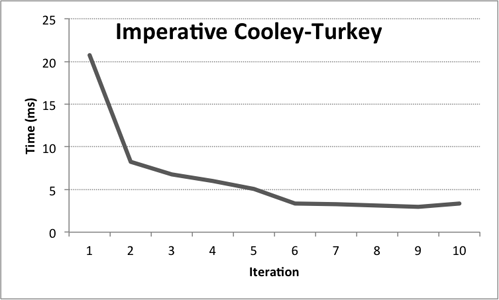
After 1000 iterations, it takes an average of ~ 0.19 ms per fft call.

Conclusions

The following table shows a side-by-side comparison of both algorithms. The times in these tables were averaged from 1000 iterations on increasing frame sizes.

Frame Size Recursive Time (ms) Imperative Time (ms)
512 1.56 0.14
1024 2.98 0.19
2048 6.04 0.27
4096 13.18 0.47

 

The imperative algorithm is clearly faster, but much more verbose and harder to understand.

Scala gets knocked sometimes for allowing both OO/imperative and functional styles of coding. In my opinion this is actually a huge benefit for the language. You can favor the functional style and resort to imperative code in cases where performance is critical. These cases can be isolated and the details can be hidden. Looking at our imperative algorithm above, the FFT is still referentially transparent.

Comments